-
1707 이분 그래프백준/그래프 이론 2024. 6. 19. 21:24
이분 그래프란,
인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프.
즉, 그래프의 모든 정점이 두 그룹으로 나눠지고 서로 다른 그룹의 정점이 간선으로 연결되어져 있는(같은 그룹에 속한 정점끼리는 서로 인접하지 않도록 하는) 그래프를 이분 그래프라고 한다.그림으로 설명하자면,

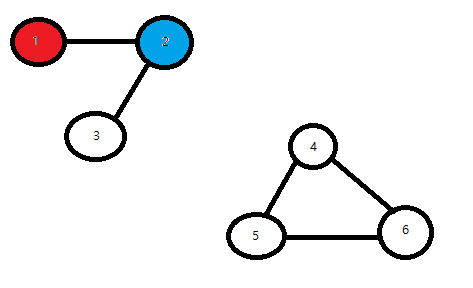
1번의 정점에 빨간색을 칠하자.

그 후 인접한 정점 2에는 다른색, 파랑색을 칠해준다.

정점 2에 인접한 3에는 빨간색을 칠해준다.

이런식으로 하다보면 결과적으로

이 그래프는 이분 그래프가 맞다.
인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프이기 때문이다.
다른 그래프를 보자면,

1번 정점에 빨간색을 칠해주고.. 순서대로 하면

1,2,3,4 정점 순서대로 색을 칠해주면 위와 같다.
하지만 4번 정점을 파랑색으로 칠한 뒤 5번 정점에 색을 칠해줘야 하는데,
빨간색을 칠할 수 없다.
5번 정점과 인접한 3번 정점이 빨간색이기 떄문에
다른 색을 칠해줘야 한다.
인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프가 될 수 없으므로

이분 그래프가 될 수 없다.
[문제 풀이]

그래프가 있다.

▶ 맨 처음 정점1을 큐에 넣고 빨간색 표시를 한다.
★ 큐 : 1
▶ 큐에서 정점 1을 꺼내고 1과 연결되어 있고 방문한 적 없는 정점 2를 큐에 넣는다. 파랑색으로 표시한다.
★ 큐 : 2

▶ 큐에서 정점 2를 꺼내고 연결된 정점 1과 3 중 3만 큐에 넣는다. 빨간색으로 표시한다.
정점 1은, 이미 방문한 적이 있으므로 정점 2와 색깔이 같은지 여부만 확인하면 된다.
색깔이 같다면 이분 그래프가 될 수 없다.
★ 큐 : 3

▶ 큐에서 정점 3을 꺼내지만, 연결된 정점 중에 방문하지 않은 정점이 없고,
색깔이 서로 다르므로 이번에는 정점 4를 큐에 넣는다.
★ 큐 : 4

▶ 큐에서 정점 4를 꺼내고 정점 5,6을 큐에 넣는다.
★ 큐 : 5,6
▶ 큐에서 정점 5를 꺼낸다. 이제 정점 5와 연결된 정점 4,6은 모두 방문한 상태이다.
이 경우 서로 색깔이 다른지 확인하면 되는데, 정점 5와 4는 색깔이 다르지만, 정점 5와 6은 색깔이 같다.
때문에 이분그래프가 될 수 없고
결과로 NO를 출력하면 된다.
☆ 색깔 칠하는 것은 배열을 이용해서, 빨간색은 값이 1, 파랑색은 값이 0
이런식으로 생각해서 풀면 된다.
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; import java.util.StringTokenizer; public class Main { static boolean visit[]; static Queue<Integer> q ; static ArrayList<ArrayList<Integer>> graph; static int color[]; static int V; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine(), " "); int K = Integer.parseInt(st.nextToken()); while(K-->0) { graph = new ArrayList<>(); q = new LinkedList<>(); st = new StringTokenizer(br.readLine(), " "); V = Integer.parseInt(st.nextToken()); int E = Integer.parseInt(st.nextToken()); for(int i=0; i<=V; i++) { graph.add(new ArrayList<>()); } for(int i= 0; i<E; i++) { st = new StringTokenizer(br.readLine(), " "); int a = Integer.parseInt(st.nextToken()); int b = Integer.parseInt(st.nextToken()); graph.get(a).add(b); graph.get(b).add(a); } visit = new boolean[V+1]; color = new int[V+1]; String result = "YES"; for(int i=1; i<=V; i++) { if(!visit[i]) { visit[i]= true; color[i] = 1; q.add(i); result = solve(i); if(result.equals("NO")) { result = "NO"; break; } } } // 이 경우 YES를 출력. System.out.println(result); } } public static String solve(int start) { String flag = "YES"; solve2: while(!q.isEmpty()) { int now = q.poll(); for(Integer next : graph.get(now)) { if(next!=0) { // 이전에 방문한 적 있다면 정점의 색깔이 다른지 여부 확인 if(visit[next]) { if(color[now] == color[next]) { flag = "NO"; break solve2; } // 이전에 방문한 적 없다면 큐에 넣고, 색깔도 바꿔주고 }else if(!visit[next]) { // 색깔 : 이전 것이 0 이면 다음은 1 // 이전 것이 1 이면 다은은 0 color[next] = 1-color[now]; visit[next] = true; q.add(next); } } } } return flag; } }
참고 블로그 : https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html
[알고리즘] 이분 그래프(Bipartite Graph)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
https://onejunu.tistory.com/112
[JAVA] 백준 1707 - 이분 그래프
www.acmicpc.net/problem/1707 1707번: 이분 그래프 입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의
onejunu.tistory.com
'백준 > 그래프 이론' 카테고리의 다른 글
18405 경쟁적 전염 (0) 2024.06.22 16928 뱀과 사다리 게임 (0) 2024.06.18 3055 탈출 (0) 2024.06.18 1068 트리 (0) 2024.06.12 14502 연구소 (2) 2024.06.10