20165 인내의 도미노 장인 호석

 

 

1. 풀이

 

이 문제에서 핵심이라고 생각한 부분을 설명하겠다.

 

문제에서 주어진 예제로 풀이한다.

 

1) map 배열

 

일단 게임판의 상태, 즉 각 격자에 놓인 도미노의 길이는

map[][] 배열에 표시한다.

그런데 크기를 [N+1][M+1] 로 했다. 

문제에서 1행 1열부터 도미노가 세워진다고 해서 

입력값이 map[1][1] 부터 map[N][M] 까지 채워지도록 했다.

 

1 1 1 1 1
1 2 2 1 1
3 1 2 2 2
1 3 2 1 1
1 3 3 1 1

 

2) result 배열

 

도미노가 넘어졌는지(F), 넘어지지 않았는지(S) 

result[][] 배열에 표시했다.

 

초기에는 도미노가 모두 서있으므로 result[][] 배열의 모든 값이 S 이다.

이 배열 크기 역시 result[N+1][M+1] 이다.

 

3) 공격수의 행동

 

<1>

문제 예시에 있는

3 1 E 를 실행하면,

(3,1) 에 있는 도미노가 오른쪽으로 쓰러진다.

그런데 이 도미노 길이가 3이다. map[3][1] = 3

 

아래 그림에서 숫자는 map[3][1] ~ map[3][5] 값으로, 즉 (3,1) ~ (3,5) 에 위치한 도미노의 길이이다.

(3,1) 의 도미노가 오른쪽으로 쓰러지면서 

(3,2), (3,3) 의 도미노가 오른쪽으로 쓰러지게 된다.

 

 

 

<2>

그런데 이 2개의 도미노도 쓰러지면서 옆의 도미노에 영향을 줄 수 있다.

(3,2) 에 위치한 도미노는 map[3][2] = 1 로,

옆에 있는 도미노에 영향을 주지 않는다.

 

 

 

 

<3>

(3,3) 에 위치한 도미노는 map[3][3] = 2 로, 오른쪽에 있는 1개의 도미노를 쓰러뜨린다.

 

 

 

정리하자면, 맨 처음 (3,1) 에 위치한 도미노가 쓰러질 때는 (3,3) 에 위치한 도미노까지 영향을 줬지만,

그로 인해 쓰러진 (3,3) 의 도미노가 (3,4) 의 도미노까지 영향을 주는 등 계속 그 범위가 늘어난다.

그래서 이를 아래와 같이 for문으로 해결했다.

 

		
		int max = b;
		int length = 0;
		
		if(direction.equals("E")) {
			
			for(int i= b; i<=max; i++) {				
				
				if(result[a][i].equals("F")) {
				
					continue;
				}
				
				result[a][i] = "F";
				count++;
				length = map[a][i];
				max = Math.max(max, length-1+i);
				max = Math.min(max, M);
				
			}
		}

 

위의 코드는 solve 메소드 내부의 for문으로, solve 메소드에는 a,b,direction 매개변수가 주어진다. 

 

위의 예제

3 1 E 를 가지고 설명하면,

a = 3, b = 1, direction = E가 된다.

 

 

* i = 1

for문은 i=1 부터 시작된다. 그리고 범위를 보면 max=1까지이다.

처음에 max = b 인데, b 값이 1이다.

핵심은 max값의 조절이다. max 값을 점차 증가시킬 수 있다.

 

i=1 일 때 for문을 실행하면,

(3,1)의 도미노를 쓰러뜨린다.  => result[3][1] = "F"

그런데, map[3][1] = 3 이므로, 오른쪽 2개의 도미노도 쓰러진다.

때문에 max 값이 3이 되어야 for문이 i=3 까지 진행되면서, (3,2), (3,3) 에 있는 도미노를 쓰러뜨릴 수 있다.

그래서 max 값을 바꾼다.

		max = Math.max(max, length-1+i);

max = Math.max(1,3-1+1) = Math.max(1,3) = 3

 

여기서 코드 아래에 보면, 

		max = Math.min(max, M);

이런 코드가 하나 더 있는데, 아래에서 설명하겠다.

 

 

 

* i = 2 

 

result[3][2] = "F" 가 된다.

map[3][2] =1 이므로 오른쪽에 있는 도미노를 쓰러뜨리지 않고, 그래서 max 값도 3으로 유지된다.

max = Math.max(3, 1-1+2) = 3

 

 

 

 

 

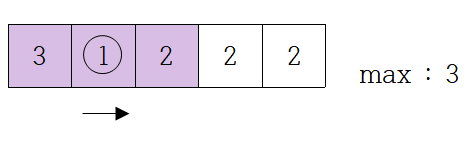
* i = 3

 

result[3][3] = "F" 가 된다.

map[3][3] = 2 이므로, 이 경우는 오른쪽 도미노를 1개 쓰러뜨린다. 그래서 max =4 가 되어야 한다.

그래야 for 문이 진행되면서 map[3][4] 도 쓰러뜨릴 수 있다.

max = Math.max(3, 2-1+3) = 4

 

 

 

 

 

이런식으로 max 값을 증가시키면서 도미노를 쓰러뜨리면 된다.

 

위에서 말했던 아래의 코드를 설명하겠다.

		max = Math.min(max, M);

도미노가 쓰러지면서 max 값이 증가될 수 있다.

그런데 만약 (3,5) 에 위치한 도미노를 쓰러뜨렸다고 하자. 

그러면 map[3][5] = 2 이므로, 오른쪽 1개의 도미노를 더 쓰러뜨리게 된다.

그런데, (3,6) 에는 도미노가 없다. 범위를 벗어나기 때문이다.

그래서 max 값을 최대 M으로 제한해주는 것이다.

 

map, result 배열의 크기는 [N+1][M+1] 로 행은 최대 N까지, 열은 최대 M까지 범위가 된다.

 

 

2. 최종 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;


public class Main {

	static int map[][];
	static String result[][];
	static int M;
	static int N;
	static int count;
	
	public static void main(String[] args) throws IOException {
		
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " " );
		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		int R = Integer.parseInt(st.nextToken());
		map  = new int[N+1][M+1];
		
		for(int i=1; i<=N; i++) {
			st = new StringTokenizer(br.readLine(), " " );
			for(int j=1; j<=M; j++) {
				map[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		
		result = new String[N+1][M+1];
		
		for(int i=0; i<=N;i++) {
			Arrays.fill(result[i], "S");
		}
		
		count = 0;
		
		for(int i=0; i<R; i++) {
			st = new StringTokenizer(br.readLine(), " " );
			int X = Integer.parseInt(st.nextToken());
			int Y = Integer.parseInt(st.nextToken());
			String D = st.nextToken();
			
			if(result[X][Y].equals("S")) {
			solve(X,Y,D);
			}
					
			StringTokenizer st1 = new StringTokenizer(br.readLine(), " " );
			int X1 = Integer.parseInt(st1.nextToken());
			int Y1 = Integer.parseInt(st1.nextToken());
			result[X1][Y1] = "S";
	
		}
		
		
		StringBuilder answer = new StringBuilder();
		answer.append(count).append("\n");
		
		for(int i=1; i<=N;i++) {
			for(int j=1; j<=M; j++) {
				answer.append(result[i][j] + " ");
			}
		
			answer.append("\n");
		}
		System.out.println(answer.toString());
	}
	
	public static void solve(int a, int b, String direction) {
		
		int max = b;
		int length = 0;
		
		if(direction.equals("E")) {
			
			for(int i= b; i<=max; i++) {				
				
				if(result[a][i].equals("F")) {
				
					continue;
				}
				
				result[a][i] = "F";
				count++;
				length = map[a][i];
				max = Math.max(max, length-1+i);
				max = Math.min(max, M);
				
			}
		}
		
		int min = b;
		
		if(direction.equals("W")) {
			for(int i= b; i>=min; i--) {
				
				if(result[a][i].equals("F")) {
				
					continue;
				}
				
				result[a][i] = "F";
				count++;
				length = map[a][i];
				min = Math.min(min, i-length+1);
				min = Math.max(1, min);
			}
		}
		
		max = a;
		
		if(direction.equals("S")) {
			
			for(int i=a; i<=max; i++) {
				
				if(result[i][b].equals("F")) {
					
					continue;
				}
				
				result[i][b] = "F";
				count++;
				length = map[i][b];
				max = Math.max(max, i+length-1);
				max = Math.min(max,N);
			}
		}
		
		min = a;
		
		if(direction.equals("N")) {
			
			for(int i=a; i>=min; i--) {
		
				if(result[i][b].equals("F")) {
						
					continue;
				}
				
				result[i][b] = "F";
				count++;
				length = map[i][b];
				min = Math.min(min, i-length+1);
				min = Math.max(1, min);
			}
		}
	}
}