크루스칼 알고리즘

 

 

1. 크루스칼 알고리즘 설명

 

 

1) 설명

 

 

- 최소 비용 신장 트리(MST, 최소 스패닝 트리) 를 찾는 알고리즘이다.

 

* 스패닝 트리 : 그래프에서 일부 간선을 선택해서 만든 트리

* 최소 스패닝 트리 : 스패닝 트리 중에서 선택한 간선의 가중치 합이 최소인 트리

 

 

- 가장 적은 비용으로 모든 노드를 연결하기 위해 사용한다.

- 정점 N 개를 가지는 그래프에서 N-1 개의 간선을 연결해야 한다.

- 모든 정점을 연결한 후 사이클이 만들어지면 안된다.

- 유니온 파인드 개념이 사용된다.

 

 

* 그래프 구성

=> 간선 : 거리, 비용 등에 해당

=> 정점

 

E : 간선의 개수

V : 정점의 개수 

 

- 크루스칼 알고리즘 시간 복잡도 : O(ElogE)

 

 

 

2) 그림을 통한 설명

 

아래와 같이 그래프가 있다고 하자.

 

 

 

 

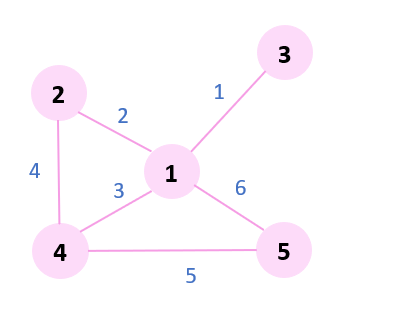
여기에는 유니온 파인드 알고리즘이 적용되기 때문에, 

각 노드의 부모 배열 parent 가 사용된다.

 

초기에는 아래와 같다.

 

 

 

크루스칼 알고리즘으로 최소 스패닝 트리를 찾아보자.

 

다음과 같은 상황으로 진행된다.

1. 모든 간선의 가중치를 기준으로 오름차순 정렬한다.

2. 정렬된 간선들의 맨 처음 값부터 차례대로 선택한다.

3. 만약 간선을 선택해서 사이클이 만들어진다면 이 간선은 건너뛰고 진행한다. => 유니온 파인드 알고리즘 사용

 

아래에서 자세히 살펴보자.

 

 

단계 1

 

간선이 가중치를 기준으로 오름차순 정렬되었다. 이 때 맨 처음 값은 가중치가 가장 작은 값이다.

즉, 1이다.

이 간선을 선택해서 사이클이 생기지 않으므로 선택한다.

 

사이클이 생기지 않는다는 것은 다음과 같다.

간선 1의 양 쪽 노드

노드 1과 노드 3에 대해서

parent 배열값이 같으면, 즉 부모가 같으면 사이클이 생긴다.

 

하지만 parent[1] =1, parent[3] = 3 으로 부모가 다르기 때문에

간선 1을 선택해도 사이클이 생기지 않는다.

그래서 간선 1을 선택한다.

그러면 유니온 파인드의 union 메소드를 통해

노드 1과 3을 합친다.

그러면 parent[1] = parent[3] =1 이 된다.

 

 

 

 

 

단계 2

 

그 다음 가중치가 작은 간선은 2이다.

역시 사이클이 생기지 않으므로 선택한다.

 

 

 

 

단계 3

 

그 다음 가중치가 작은 것은 3이다.

역시 사이클이 생기지 않으므로 선택한다.

 

 

 

단계 4

 

간선 4를 선택하면 사이클이 생긴다.

 

즉, 양쪽 노드인 2와 4의 부모가 같다.

parent[2] = 1

parent[4] = 1

 

그래서 사이클로 생기므로

선택하지 말고 다음 단계로 넘어간다.

 

 

 

단계 5

 

그 다음 간선 5를 선택하면 사이클이 생기지 않는다.

간선 5를 선택한다.

 

 

 

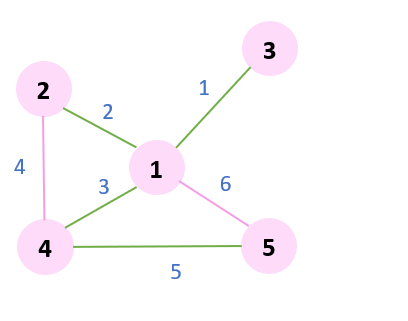
단계 6

 

간선 6을 선택하면 사이클이 생긴다.

양쪽 노드인 1과 5의 부모가 같다.

parent[1] = 1

parent[5] = 1

 

간선 6을 선택하지 말고 끝이난다.

 

그러면 다음과 같은 최소 스패닝 트리가 만들어진다.

 

 

 

그리고 이렇게 만들어진 최소 스패닝 트리의 간선들의 합은

11이 된다.

 

2. 최종 코드

 

import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;

public class Main {

	static class Edge {
		int a;
		int b;
		int cost;
		
		Edge(int a, int b, int cost) {
			this.a = a;
			this.b = b;
			this.cost = cost;
		}
	}

	static int parent[];
	
	public static void main(String[] args) throws IOException {
		
		parent = new int[6];
		
		for(int i=1; i<6; i++) {
			parent[i] = i;
		}
		
		ArrayList<Edge> list = new ArrayList<>();
		
		list.add(new Edge(1,2,2));
		list.add(new Edge(1,3,1));
		list.add(new Edge(2,4,4));
		list.add(new Edge(1,4,3));
		list.add(new Edge(1,5,6));
		list.add(new Edge(4,5,5));
		
		Collections.sort(list, new Comparator<Edge>() {
			
			@Override
			public int compare(Edge e1, Edge e2) {
				if(e1.cost < e2.cost) {
					return -1;
				}else {
					return 1;
				}
			}
		});
		
		
		int sum = 0;
		
		for(int i =0; i< list.size(); i++) {
			
			Edge edge = list.get(i);
		
			if(!solve(edge.a , edge.b)) {
				sum+= edge.cost;
				union(edge.a,edge.b);
				
			
			}
		}
		
		System.out.println(sum);

	}
	
	
	public static int find(int x) {
		if(x == parent[x]) {
			return x;
			
		}else {
			return parent[x] = find(parent[x]);
		}
	}
	
	public static void union(int x, int y) {
		x = find(x);
		y = find(y);
		
		
		if(x<y) {
			parent[y] = x;
		}else {
			parent[x] = y;
		}
	}
	
	public static boolean solve(int x, int y) {
		
		x = find(x);
		y = find(y);
		
		if( x==y) {
			return true;
			
		}else {
			return false;
			
		}
	}
}

 

 

참고 블로그 :

 

https://born2bedeveloper.tistory.com/31

[JAVA] 크루스칼 알고리즘(Kruskal Algorithm)

 

https://brenden.tistory.com/36

[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)