6588 골드바흐의 추측

 

 

1. 풀이

 

에라토스테네스의 체 알고리즘에 대해 먼저 설명하겠다.

 

소수를 판별하는 알고리즘이다.

 

만약 20까지의 숫자에 대해서 소수를 판별해보자면 다음과 같다.

 

아래 그림에서 소수만 남겨보도록 하자.

 

 

 

1.

일단 소수는 1보다 큰 양의 정수이므로, 1을 지워준다.

 

 

2.

그 후 2를 제외한 2의 배수를 지워준다.

 

 

 

3.

이번에는 3을 제외하고 3의 배수를 지워준다.

 

 

 

 

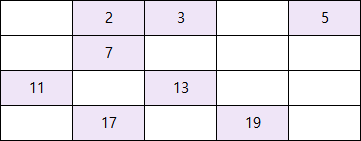
4.

4는 이미 2의 배수로 지워졌기 때문에 5로 넘어간다.

 

 

5.

5를 제외하고 5의 배수를 지워준다. 

 

5를 제외한 5의 배수도

2와 3의 배수 때 지워져서

아래처럼 그대로이다.

 

 

 

이런 식으로 지워나가면 된다.

 

코드에 보면 number 배열이 있는데, 

소수이면 true 가 표시된다.

즉, 위의 과정에서

최종 남은 숫자들은 number 배열 값이 true 이다.

 

 

이렇게 에라토스테네스의 체 알고리즘을 이용해서

소수 판별을 하고 난 다음에는

 

각 입력값 n을 a+b 형태로 나타내야 한다.

그런데 문제에서 n을 만들 수 있는 방법이 여러 가지라면 

b-a 가 가장 큰 것을 출력하라고 했다. 

그러면 a는 제일 작고, b는 제일 큰 소수를 찾으면 된다.

 

따라서 a는 2부터 시작해서 점점 증가시키면서 소수인지 확인하고,

b = n- a 이므로 b도 소수인지 확인한 뒤,

맞다면 정답이 된다.

 

 

2. 최종 코드

 

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {
	
	public static void main(String[] args) throws IOException {
		
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));		
		int max = 1000000;
		boolean number [] = new boolean[max+1];
		
		Arrays.fill(number, true);
		number[0] = false;
		number[1] = false;
		
		for(int i = 2; i<=max; i++) {
			
			if(!number[i]) {
				continue;
				
			}else {
				
				for(int j = i+i; j<=max; j+=i) {
					number[j] = false;
				}
			}
		}
	
		while(true) {
			
			int n = Integer.parseInt(br.readLine());
			if(n==0) {
				break;
			}
		
			for(int i = 2; i<=n; i++) {
			
				if(i ==n ) {
					System.out.println("Goldbach's conjecture is wrong");
				}
				
				if(number[i]  && number[n-i]) {
				
					int a = i;
					int b = n-i;
					System.out.println(n + " = " + a + " + " + b);
					break;
				}
			}
		
		}
	}
}

 

참고 블로그 :

 

https://brenden.tistory.com/48

[알고리즘] 에라토스테네스의 체(Sieve of Eratosthenes)