10164 격자상의 경로

 

 

1. 풀이

 

 

문제에 주어진 예시를 가지고 설명하겠다.

 

3 5 8

 

이러한 값이 주어졌기 때문에 격자는

 

이와 같다.

map[i][j] 배열에 위와 같이 입력한다.

 

dp[i][j] 배열은

처음 위치(0,0) 에서 ((i,j) 위치까지 이동하는 서로 다른 경로의 수를 입력할 것이다.

 

그러면 8의 위치를 변수 a,b 에 저장한다.

즉, 8의 위치는 (1,2) 이다.

a = 1, b = 2

 

1) 

 

dp[0][1] ~ dp[0][b] = 1  

 

=> dp[0][1] = 1 인건,

(0,0) 에서 출발해서 (0,1) 까지 이동가능한 방법은

오른쪽으로 이동하는 경우 1가지 있다.

 

=> dp[0][2] = 1 인건,

(0,0) 에서 출발해서 (0,2) 까지 이동가능한 방법이

오른쪽으로 이동하는 경우 1가지 있기 때문이다.

 

dp[1][0] ~ dp[a][0] = 1

 

=> 이 경우도 (0,0) 에서 출발해서 아래로 이동하는 경우 1가지 있다.

 

2) 

 

dp[1][1] ~ dp[a][b] 까지

 

dp[i][j] = dp[i-1][j] + dp[i][j-1]

 

이 식을 통해서 값을 채운다.

 

예를 들어서 dp[1][1] = dp[0][1] + dp[1][0] 이다.

 

즉,

(0,0) 에서 (1,1) 로 가는 경로의 수

= (0,0)에서 (0,1) 로 가는 경로의 수 + (0,0)에서 (1,0) 로 가는 경로의 수이다.

3) 

 

dp[a][b+1] ~ dp[a][M-1] = 3

 

dp[a+1][b] ~ dp[N-1][b] = 3 

 

 

 

 

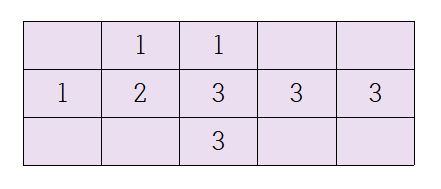
(a,b) 위치에서 (N-1, M-1) 위치까지 서로 다른 경로의 수를 찾아야 한다.

 

 

이때 위에서 

dp[i][j] = dp[i-1][j] + dp[i][j-1] 이라고 했다.

즉, 

 

 

(0,0)에서 (1,3) 까지 이동하는 경로의 수 => 9까지 이동

= (0,0)에서 (1,2) 까지 이동하는 경로의 수 => 8까지 이동

+ (0,0)에서 (0,3)까지 이동하는 경로의 수  -> 4까지 이동

 

그런데, 8을 반드시 지나가야 하기 때문에, 4로 이동하는 경로의 수는 없다.

그래서, 9까지 이동하는 경로의 수는 8까지 이동하는 경로의 수와 같다.

 

 

4) 

 

dp[a+1][b+1] ~ dp[N-1][M-1] 은

 

dp[i][j] = dp[i-1][j] + dp[i][j-1] 

 

식으로 채우면 된다.

 

 

 

 

 

5)

 

정답은

dp[N-1][M-1] 이 된다.

 

 

2. 최종 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;


public class Main {
	
	public static void main(String[] args) throws IOException {
		
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " " );
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());
		int K = Integer.parseInt(st.nextToken());
		
		int map[][] = new int[N][M];
		
		int a = 0;
		int b = 0;
		
		if(K==0) {
			a = N-1;
			b = M-1;
		}
		
		int dp[][] = new int[N][M];
		
		int number = 1;
		
		for(int i = 0; i < N; i++) {
		
			for(int j = 0; j < M; j++) {
			
				map[i][j] = number;
				
				if(map[i][j] == K) {
					a = i;
					b = j;
				}
				
				number++;
			}
		}
		
		
		for(int i = 1; i <= b; i++) {
		
			dp[0][i] = 1;
		}
		
		for(int i = 1; i <= a; i++) {
			
			dp[i][0] = 1;
		}
		

		for(int i = 1; i <= a; i++) {
			
			for(int j = 1; j <= b; j++) {
			
				dp[i][j] = dp[i-1][j] + dp[i][j-1];
			
			}
		}
		
		
		for(int i = b; i < M; i++) {
			
			dp[a][i] = dp[a][b];
		}
		
		for(int i = a; i < N; i++) {
			
			dp[i][b] = dp[a][b];
		}
		

		for(int i = a; i < N; i++) {
		
			for(int j = b; j < M; j++) {
				
				if(i-1 >= 0 && j-1 >= 0) {
			
					dp[i][j] = dp[i-1][j] + dp[i][j-1];
			}
	      }
		}
	
		
		System.out.println(dp[N-1][M-1]);
     }
  }