버블 정렬

 

1. 버블 정렬

 

버블 정렬은 다음과 같이 진행된다. (오름차순 기준)

 

1. 맨 앞 숫자(a) 부터 비교를 시작한다.

 

2. 바로 뒤의 숫자(b) 와 비교해서 뒤의 숫자가 더 작으면 자리를 바꿔준다.

 

즉, a b 순서였는데

b < a  이면 b a 로 자리를 바꿔준다.

 

3. 그 다음 숫자와 비교하면서 위와 같은 과정을 반복한다.

 

4. 맨 끝까지 비교가 끝나면 다시 맨 앞 숫자를 뒤의 숫자와 비교한다.

 

 

시간 복잡도

최선의 경우 : O(N)

평균 : O(N*N)

 

단점 : 다른 정렬 알고리즘에 비해 교환과정이 많아서 시간 소비가 크다.

 

 

2. 그림으로 설명

다음과 같은 상황이라고 하자.

 

 

단계 1

 

 

 

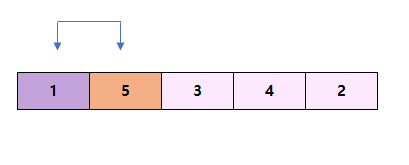
맨 앞에 있는 값은 1이다.

바로 뒤의 5와 비교한다.

5가 더 크므로 둘의 자리를 그대로 둔다.

 

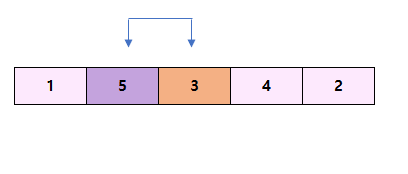
그 다음 5와 3을 비교해서 5가 더 크므로 자리를 바꾼다.

 

 

 

5보다 4가 작으므로 자리를 바꿔준다.

 

 

 

5보다 2가 작으므로 자리를 바꿔준다.

 

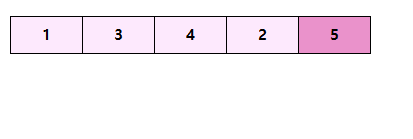
그럼 이제 끝이났다.

맨 마지막에 위치한 5는 이제 확정이 되었다.

 

 

 

단계 2

 

또 다시 맨 앞에 있는 값과 뒤의 값을 비교한다.

1과 비교해서 3이 크기 때문에, 그대로 두면 된다.

 

 

 

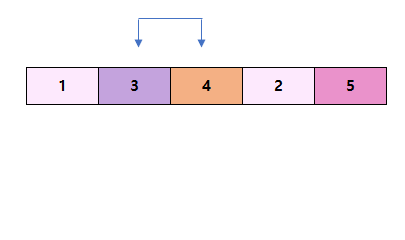
역시 그대로 두면 된다.

 

자리를 바꿔준다.

 

5는 이미 단계 1에서 확정되었기 때문에 4,5를 비교할 필요 없다.

4도 확정된다.

 

단계 3

 

 

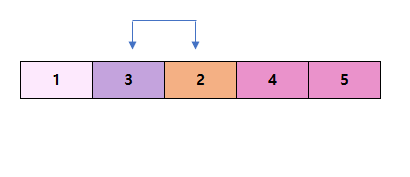
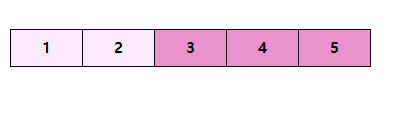
단계 4

 

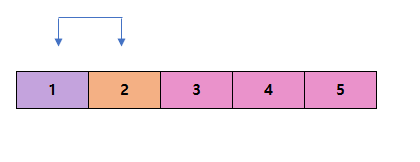
결론

 

단계를 진행할 때마다 뒤에서 한 개씩 정렬되기 때문에 

비교하는 횟수가 점점 줄어들게 된다.

 

 

3. 최종 코드 

 

1) 시간 복잡도 : O(N*N) 

 

import java.io.IOException;
import java.util.Arrays;


public class Main {
	
	public static void main(String[] args) throws IOException {
		
		int a[] = {1,5,3,4,2};
		
		int size = 5;
		
		for(int i =1; i< size; i++) {
			
			for(int j =0; j<size - i; j++) {
				
				if(a[j] > a[j+1]) {
					
					int value = a[j];
					a[j] = a[j+1];
					a[j+1] = value;
					
				
				}
			}
		}
		
		System.out.println(Arrays.toString(a));
	}
}

 

 

2) 시간 복잡도 : O(N) - 최선의 경우 , O(N*N)  - 최악의 경우 

 

 

위에서 최선의 경우에는 시간복잡도가 O(N) 이라고 했다.

최선의 경우는 1 2 3 4 5 가 있겠다.

이미 정렬이 되어 있는 상태이다.

 

그런데 위의 코드로는 최선의 경우에도 O(N*N) 이 된다.

 각 단계마다 앞에 있는 숫자가 큰 지 뒤에 있는 숫자가 큰지 비교해야 되기 때문이다.

 

그래서 다음과 같은 코드를 만들어서,

각 단계에서 숫자들의 대소 비교한 뒤, 

그 단계에 모두 정렬되어 있다는 것이 판단되면

정렬을 종료하도록 한다.

 

즉 아래의 코드는

boolean 형 변수 check 를 사용한다.

그리고 처음에 check = false 로 초기화한다.

 

단계 1은

맨 처음 숫자부터 마지막까지 앞, 뒤 숫자의 대소를 비교한다.

그런데 만약

입력값이 1 2 3 4 5 라면 

정렬이 된 상태이므로 

앞 뒤 위치가 바뀌는 일이 없을 것이다.

 

그러면 check = false로 변함없게 한다.

 

즉, 단계 1을 진행한 뒤 여전히 check = false 라면

단계 2로 넘어가는게 아니라

반복문을 종료해서 정렬을 끝내는 것이다.

즉 이렇게 되면 시간 복잡도는 O(N) 을 만족한다.

 

하지만 입력값이

5 4 3 2 1 이라면,

정렬이 필요하고,

단계 1에서 숫자들의 위치를 바꿔줘야 한다.

 

이렇게 바꾸는 상황이 생기면 check = true 로 바꿔서,

반복문이 끝나지 않고 정렬을 계속 진행되도록 하면 된다.

이 경우도 물론 최악의 경우는 O(N*N) 이 발생할 수 있다.

 

 

 

 

import java.io.IOException;
import java.util.Arrays;


public class Main {
	
	public static void main(String[] args) throws IOException {
		
		int a[] = {1,2,3,4,5};
		
		int size = 5;
		
		for(int i =1; i< size; i++) {
			
			boolean check = false;
			
			for(int j =0; j<size - i; j++) {
				
				if(a[j] > a[j+1]) {
					
					int value = a[j];
					a[j] = a[j+1];
					a[j+1] = value;
					
					check = true;
				}
			}
			
			
			
			if(check==false) {
				break;
			}
		}
		
		System.out.println(Arrays.toString(a));
	}
}

 

 

 

 

참고 블로그 : 

 

https://st-lab.tistory.com/195